Do the Math: Make Mathematics in Wikipedia Computable
This wiki supports our submission to the IEEE TPAMI journal: "Do the Math: Making Mathematics in Wikipedia Computable" [1]. For legal inquiries, use the methods described at https://wikitech.wikimedia.org/.
In the following, we demonstrate the capabilities of our system based on a subset of articles copied from the English version of Wikipedia. The full list of all demo pages can be viewed here: Special:AllPages (excluding the benchmark entries named with Gold). On this main page, we explain how you can explore our demo pages and interact with our translation and evaluation pipeline. Afterward, we provide more detailed explanations to certain topics that did not fit into the paper. Those sections are also available in the supplementary materials.
Sincerely, the authors.
Explore the Demo
Click on a Formula

Each page in this Wiki is semantically enhanced with our tool. You can go to any of our demo pages and click on a formula. This triggers our semantification, translation, and evaluation pipeline and leads to a page that shows you the generated information for the formula you clicked. As a good starting point, you can go to our use case example about Jacobi polynomials and click on the definition of the Jacobi polynomials.
The Jacobi polynomials are defined via the hypergeometric function as follows:
where is Pochhammer's symbol (for the rising factorial).
The information and translations are generated based on the context of the formula, i.e., the article in which the formula appeared. Consequently, clicking on the same formula in different articles may yield different results. Because of limited resources, sometimes, calculations are not applied in some CAS. So if the special page shows numeric test calculations just for one CAS, the other CAS ran out of memory at the same time.
Setup Your Own Scenario
In addition, you can go to the custom page directly and enter your own context and formula. Note that the given formula does not necessarily need to be in the provided context. Since the formula will be integrated into the dependency graph first, the necessary descriptive terms will be extracted from the ingoing dependencies. The screenshot to the right shows a custom example for with a simple, single sentence context. Even though the formula itself does not appear in the context, the dependency graph establishes ingoing dependencies and .
Interpreting the Results

The result page shows various information about the clicked (enhanced) formula including the original TeX, the rendered form, the semantic LaTeX form, and a confidence score (the score is explained in the paper).
Below this general information follow CAS-specific translation and evaluation information. The screenshot on the right shows the first part of the results for the custom example from the previous section.
It shows the translation to Mathematica, followed by information about the translation process. Those are subequations (in case multiple equations appeared in that formula), the extracted free variables, and translation decisions. For example, it shows that the Pochhammer symbol was translated to the pattern Pochhammer[$0, $1]. Below the translation, information follows the evaluation results. First the symbolic evaluation with the tested expression (left-hand side minus right-hand side of the subequation). The test was successful because FullSimplify[(Pochhammer[z, n])-(Divide[Gamma[z + n],Gamma[z]])] returned . The numeric evaluation shows 10 test values of which all 10 were successful. The actual qualitative evaluation was performed on more test values. For this online demo, we limit the evaluation pipeline to 10 test cases.
By clicking on Expand at the right of each test case, we can retrieve more information. The first test calculation, for example, was computed for n=1 and z=E^((I/6)*Pi) and returned 1.1102230246251565*^-16 - 5.551115123125783*^-17*I which is not exactly zero due to machine accuracy limitations. Nontheless, the result was below the threshold and counted as successful.
The same information is provided for Maple. In some cases, a translation to SymPy is also presented. However, the SymPy support is still very limited. Hence, most cases show an empty translation and evaluation for SymPy. Due to memory issues in our Docker environment, Maple may crash which results in aborted numeric test cases.
Noun Phrase Definition
Originally, we considered only nouns, noun sequences, adjectives followed by nouns, and Wikipedia links as candidates of definiens[1].
However, in the field of OPSF, such descriptions are generally insufficient.
Hence, we include connective possessive endings and prepositions between noun phrases (see supplementary materials for further details).
Consider the Bessel functions of which there are two kinds, the first and the second. Additionally, there are modified and spherical versions, each with a first and second kind.
Hence, in order to distinguish one from another, we need to know the entire name, such as the \textit{modified Bessel function of the second kind}.
Thence, we define our MC as noun phrases NP in terms of POS tag patterns used by CoreNLP.
We use the following patterns: (1) JJ* NN+, (2) JJ* NN+ POSS NN+, and (3) JJ* NN+ IN DT? JJ* NN+.
The POS tags refer to the tags used by CoreNLP and JJ and NN include all specialized forms (such as plurals NNS).
The symbols ?, +, and * refer to the quantities at most once, at least once, and many or none of the successive tokens with that particular POS tag.
These new noun phrase definitions allow us to distinguish special functions and orthogonal polynomials more adequately in contrast to the previously used nouns, noun sequences, and adjective-noun sequences.
Note that a noun phrase may appear multiple times in a document.
In that case, we adjusted the score as in[2].
While we have not found any improvement in the original project on single identifiers[2], this score adjustment performs better on our current use case.
Note that MLP also tries to increase the score if a noun phrase appears multiple times in the same list. This happens if the same description occurs multiple times near the same MOI. While Schubotz et al.[2] reported that this adjustment did not lead to better performance, we identified the opposite in our use cases and include the proposed adjustment for the score calculations.
Translation Pipeline

n(x) would be annotated with all descriptive terms (green) from the sentence in the introduction and the sentence in the definition of the Jacobi polynomial.

In the following, we briefly explain the translation process in an example. Because of page limitations, we did not put the example in our submission. This section is also given in the supplementary materials.
Example Translation
Consider the English Wikipedia article about Jacobi polynomials as our exemplary use case. The Figure on the right shows the dependency graph overlay for the first equation in that article. Due to implementation constraints and performance reasons, the implementation of our demo page slightly differs from the actual pipeline we used internally. The only difference is that the given formula does not need to be in the given context. The reason is, that we can build a dependency graph of the given context first and then ask for a single formula translation and computation. This is more efficient compared to translating and computing an entire document at once. So the actual pipeline you can use in our demo works as follows. First, a dependency graph is generated for the page that serves as our context. Next, the given formula is integrated into the dependency graph. If the given formula is already in the graph, we can work with that node. If not, we generate a new node and set up the dependencies for this new node. Consider, we want to translate the equation
in the context of Jacobi polynomials. Since this equation does exist in the context, we take that node in the dependency graph for the following process. The dependency graph from Jacobi polynomials tells us, that the equation contains two other MOI, namely from earlier in the article and right below the equation, while the definition itself is not part of any other MOI (no outgoing dependencies). Hence, the annotated descriptive terms for the equation are only the noun phrases extracted from the sentence the equation appears in. These noun phrases are Pochhammer's symbol (0.69), hypergeometric function (0.6), and Jacobi polynomial (0.6). Note that the term rising factorial at the end of the sentence is not included. Because of the aforementioned challenges in processing mathematical language (see Section 2.1 in our paper), CoreNLP tagged factorial as an adjective instead of a noun and, therefore, the phrase was not considered as a noun phrase.
Next we search for semantic macros with the descriptive terms annotated to the definition in the dependency graph and find \JacobipolyP for Jacobi polynomials, \Pochhammersym for the Pochhammer's symbol, and \genhyperF for hypergeometric function. Each retrieved macro contains a list of possible replacement patterns. Finally, we score each replacement pattern by the score that was generated from MLP for the descriptive term, the search score from ES for retrieving the macro, and the likelihood value of the semantic macro version in the DLMF. Finally, we iterate over every in-going dependency of the MOI and recursively apply the same process to each of the dependant MOIs. For the equation above, this recursive behavior would not be necessary since every component of the equation is already mentioned in the same sentence. However, consider as a counterexample the next equation in the same article
In the context of this equation, neither the Jacobi polynomial nor the Gamma function is mentioned in the sentence. However, iterating over the ingoing dependencies reveals from later in the article and from the introduction. Both MOI are annotated with the necessary descriptions to retrieve the replacement patterns for the gamma function and the Jacobi polynomial. Finally, we order the list of retrieved replacement patterns according to their scores. The score for a single replacement pattern is the average of the scores from each part of the retrieval pipeline. Those are (1) the noun phrase score for the given formula calculated from MLP, (2) the relative Elasticsearch score of the retrieved semantic macro replacement patterns, and the DLMF likelihood values for each generic LaTeX pattern. The following table contains some of the retrieved replacement rules.
We apply each replacement pattern that we extracted (table above). The replacement patterns for \JacobipolyP, \Pochhammersym, and \genhyperF matched parts in the original LaTeX (green backgrounds in the table above).
The original LaTeX looks like this:
P_n^{(\alpha,\beta)}(z)=\frac{(\alpha+1)_n}{n!}{}_2F_1\left(-n,1+\alpha+\beta+n;\alpha+1;\tfrac{1}{2}(1-z)\right)
The replacement patterns replaced each part with the semantic macros. Hence, the semantically enhanced (or simply semantic LaTeX) looks like this:
\JacobipolyP{\alpha}{\beta}{n}@{z} = \frac{\Pochhammersym{\alpha + 1}{n}}{n!}\genhyperF{2}{1}@{-n,1+\alpha+\beta+n}{\alpha+1}{\tfrac{1}{2}(1-z)}
Every semantic macro in this expression is supported by LaCASt. Hence, we can now use LaCASt to translate it to Maple
JacobiP(n, alpha, beta, z) = (pochhammer(alpha + 1, n))/(factorial(n))*hypergeom([- n , 1 + alpha + beta + n], [alpha + 1], (1)/(2)*(1 - z))
and Mathematica
JacobiP[n, \[Alpha], \[Beta], z] == Divide[Pochhammer[\[Alpha]+ 1, n],(n)!]*HypergeometricPFQ[{- n , 1 + \[Alpha]+ \[Beta]+ n}, {\[Alpha]+ 1}, Divide[1,2]*(1 - z)]
In addition, we automatically evaluate the equation numerically and symbolically as described in the supplementary material. Essentially, LaCASt extracted 4 free variables in the expression: , , , and . Further, it located the equal sign to split the expression in left- (LHS) and right-hand side (RHS). The symbolical test tries to simplify the difference of LHS and RHS to 0. For Mathematica, this looks like
FullSimplify[(JacobiP[n, \[Alpha], \[Beta], z])-(Divide[Pochhammer[\[Alpha]+ 1, n],(n)!]*HypergeometricPFQ[{- n , 1 + \[Alpha]+ \[Beta]+ n}, {\[Alpha]+ 1}, Divide[1,2]*(1 - z)])]
Since it is the common definition of Jacobi polynomials, Mathematica indeed returns 0 for this simplification. Hence, the symbolic test was successful. The numeric tests work similarly. We replace every variable with actual numeric values and calculate the difference between LHS and RHS. If the numerically calculated difference is 0, the test was successful. Because of resource limitations, we limit the number of test calculations to 10. For example, in Maple, one of the test calculations was for . The difference of LHS and RHS for these values was , which is equal to 0. Hence the numeric test was successful for this particular case. All other test calculations were also successful. Conclusively, the entire numeric test case was successful. The evaluation results for this particular example can be found on the demo page for the equation above: [2].
Automatic Symbolic and Numeric Evaluation Pipeline
The numeric and symbolic evaluation pipeline was first introduced and performed on the DLMF. Formulae in the DLMF are encoded in semantic LaTeX and annotated with additional information, such as constraints. Constraints are crucial to avoid calculations on invalid values. Currently, we are unable to retrieve constraints from Wikipedia articles. Hence, we can expect a lower verification rate compared to evaluations on the DLMF. In the following, we briefly explain the symbolic and numeric evaluation more in detail. A more detailed explanation of the pipeline and the results of the evaluation of the entire DLMF have been submitted to the international conference on tools and algorithms for the construction and analysis of systems and will be linked here once available.
A case analyzer first splits multiple relations in a single line into multiple test cases. Note that only the adjacent relations are considered, i.e., with , we generate two test cases and but not . In addition, expressions with and are split accordingly, e.g., is split into and . On the DLMF, LaCASt is able to automatically resolve most substitutions due to annotated links on each formula. In the future, we plan to mimic the internal links in the DLMF with our generated dependency graph. After generating the test case, we translate the expression to the CAS representation. Every successfully translated test case is then symbolically verified, i.e., the CAS tries to simplify the difference of an equation to zero. Non-equation relations simplifies to Booleans. Non-simplified expressions are verified numerically for manually defined test values, i.e., we calculate actual numeric values for both sides of an equation and check their equivalence.
The symbolic evaluation was performed for Maple as in[3]. However, we use the newer version Maple 2020. Another feature we added to LaCASt is the support of packages in Maple.
Some functions are only available in modules (packages) that must be preloaded, such as QPochhammer in
the package QDifferenceEquations[3].
The general simplify method in Maple does not cover q-hypergeometric functions.
Hence, whenever LaCASt loads functions from the q-hyper-geometric package, the better
performing QSimplify method is used.
With the Wolfram Engine for Developers
(WED)[4] (hereafter, with Mathematica, we refer to the WED) and the new support for Mathematica in LaCASt, we perform the symbolic and numeric
tests for Mathematica.
The symbolic evaluation in Mathematica relies on the full simplification[5].
For Maple and Mathematica, we defined the global assumptions and
.
Constraints of test cases are added to their assumptions to support simplification. Adding more global assumptions for symbolic computation generally harms the performance since CAS internally uses assumptions for simplifications. It turned out that by adding more custom assumptions, the number of successfully simplified expressions decreases.
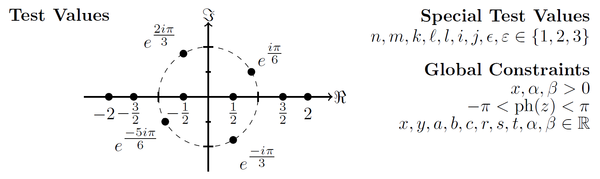
Defining an accurate test set of values to analyze an equivalence can be an arbitrarily complex process. It would make sense that every expression is tested on specific values according to the containing functions. However, this laborious process is not suitable for evaluating the entire datasets or CAS. It makes more sense to develop a general set of test values that (i) generally covers interesting domains and (ii) avoid singularities, branch cuts, and similar problematic regions. Considering these two attributes, we come up with the ten test points illustrated in the Figure above. It contains four complex values on the unit circle and six points on the real axis. The test values cover the general area of interest (complex values in all four quadrants, negative and positive real values) and avoid the typical singularities at .
The numeric evaluation engine heavily relies on the performance of extracting free variables from an expression. Unfortunately, the inbuilt functions in CAS, if available, are not very reliable.
As the authors explained in[3], a custom algorithm within Maple was necessary to extract identifiers. Mathematica has the undocumented function Reduce`FreeVariables for this purpose.
However, both systems, the custom solution in Maple and the inbuilt Mathematica function, have problems distinguishing free variables of entire expressions from the bound variables in sums, integrals, and similar operations.
Since the extended version of LaCASt handles operators, including bound variables of sums and integrals, we drop the use of internal methods in CAS and extend LaCASt to extract identifiers from an expression. During a translation process, LaCASt tags every single identifier as a variable, as long as it is not an element of a math operator such as sum or integral. This simple approach proves to be very efficient since it is implemented alongside the translation process itself and is already more powerful compared to the existing inbuilt CAS solutions.
We defined subscripts of identifiers as a part of the identifier, e.g., and are
extracted as variables from rather than .
The general pipeline for a numeric evaluation works as follows.
First, we extract the variables from the
left- and right-hand sides of the test expression via LaCASt.
For the previously mentioned example of the definition of the Jacobi polynomial,
LaCASt identifies four variables in the expression, , , , and .
According to the values in the Figure to the right, only is set to the general ten values, while is and are the six values on the real axis .
A numeric test contains every combination of test values for all variables.
Hence, we start generating test calculations.
Afterward, we filter the test values that violate the attached or global constraints.
In the case of the Jacobi polynomial, we end up with 10 values for , 6 each for and , and 3 for .
Hence, we end up with 1080 test calculations.
Due to limitations for our online demo, we limit the test calculations to 10 for each test case, i.e., we took the first 10 generated cases only.
Finally, we calculate the result for every remaining test value, i.e., we replace every variable by their value and calculate the result.
The replacement is done by Mathematica's ReplaceAll method because the more appropriate method With, for unknown reasons, does not always replace all variables by their values.
We wrap test expressions in Normal for numeric evaluations to avoid conditional expressions, which may cause incorrect calculations.
After replacing variables with their values, we trigger numeric computation.
If the absolute value of the result is below the defined threshold of 0.001 or true (in the case of inequalities), the test calculation is considered successful.
A numeric test case is only considered successful if and only if every test calculation was successful.
If a numeric test case fails, we store the information on which values it failed and how many of these were successful.
Evaluation Analysis
In this section, we refer to a benchmark entry with the associated ID. The full benchmark dataset can be found at Poject:GoldData. In the following, we discuss some issues we identified with the evaluation. This section is more comprehensive to the one in the paper. It also contains some actual examples and direct links to the entries.
False Math Detection
Since the benchmark contains randomly picked formulae from the articles, it also contains entries that might not have been properly annotated with math-templates or math-tags in the Wikitext. Four entries in the benchmark (28, 43, 78, and 85) were wrongly detected by our engine and contained only parts of the actual formula. For example, entry 28 was extracted as _{1}(z) = from the Polylogarithm because the formula was given in plain text Li<sub>1</sub>(''z'') = -ln(1-''z''). While our approach correctly identified <sub>1</sub>(''z'') = and (1-''z''), it did not identify the plain text words Li and ln as part of the formula.
Inappropriate LaTeX
Some translations also failed due to inappropriate LaTeX expressions. For example, the hypergeometric functions have an index prior to the identifier , such as in . In many cases, the leading subscript was attached to the previous token, such as equal signs (84) or asterisks for multiplications (75, 83), rather than using an empty expression {}_{1}. For example, entry 75
Here the asterisk has an index: (*_4). Hence, we were not able to match with \qgenhyperphi{4}{3}@... because the DLMF macro pattern presumed an empty expression with underscore rather than an asterisk.
In one case (85) (from Continuous q-Laguerre polynomials), the editor of the Wikipedia article even split the entire equation into two parts via </math><math> to avoid the problem with the leading underscore. Hence, our extracted formula was not complete and missed the second half of the expression.
<math>P_{n}^{(\alpha)}(x|q)=\frac{(q^\alpha+1;q)_{n}}{(q;q)_{n}}</math><math>_{3}\Phi_{2}(q^{-n},q^{\alpha/2+1/4}e^{i\theta},q^{\alpha/2+1/4}*e^{-i\theta};q^{\alpha+1},0|q,q)</math>
Definitions and Substitutions
Recognizing an equation as a definition would have a great impact on performance. As a test, we manually annotated every definition in the benchmark by replacing the equal sign = with the unambiguous notation and extended LaCASt to recognize such combination as a definition of the left-hand side (the DLMF did not use this notation, hence LaCASt was not capable of translating in the first place). This resulted in 18 more correct translations (e.g., 66, 68, and 75) and increased the performance from .28 to .47.
Identifying definitions in a document would also solve the problem of substitutions. Consider, for example, the benchmark entry 3 containing the elliptic integral of the first kind , from the article Elliptic integral. Here, x was defined as the Jacobian elliptic function immediately above this equation. Hence, an appropriate translation of to Mathematica would be
EllipticF[ArcSin[JacobiSN[u, (k)^2]], (k)^2] == u
While LaCASt is capable of performing such complex translation from semantic LaTeX (note that the second arguments are squared and we must use for the first argument), we were not able to detect the substitution of . Hence, our translation was not appropriate, as defined in our paper.
The dependency graph may provide beneficial information towards a definition recognition system for equations. However, rather than presuming that every equation symbol is indicating a definition[4], we propose a more selective approach. Considering one part of an equation (including multi-equations) as an extra MOI would establish additional dependencies in the dependency graph, such as a connection between and . A combination with recent advances of definition recognition in NLP [5] [6] [7] [8] may then allow us to detect x as the defining element. The already established dependency between x and can finally be used to resolve the substitution. Hence, for future research, we will elaborate the possibility of integrating existing NLP techniques for definition recognition[5][6] into our dependency graph concept.
Missing Information
Another problem that causes translations to fail is missing information. For example, the gamma function seems to be considered common knowledge in most articles on special functions because it is often not specifically declared by name in the context (e.g., 19, 31, and 53). To test the impact of considering the gamma function as common knowledge, we added the description Euler gamma function to the list of noun phrases that fetch semantic macros from the database. Adding a low score ensures the pattern for the gamma function will be applied late in the list of replacement patterns. This indeed improved performance slightly, providing us a successful translation of three more benchmark entries (19, 56, and 93). Additionally, it improved the semantic LaTeX in three other entries (22, 31, and 53) but these cases had other issues that prevented a successful translation. This naive approach, emphasizes the importance of knowing the domain knowledge for specific articles. Schubotz et al.[1] utilized namespaces of mathematical expressions to improve definiens extractions for identifiers. These namespaces may allow us to activate the feature we used to test the impact of the gamma function more precisely in certain cases and deactivate it in others.
Non-Matching Replacement Patterns
An issue we would more regularly face in domains other than special functions and orthogonal polynomials are non-standard notations. For example, for six entries (18, 44, 59, 62, 77, and 87) we were not able to appropriately replace hypergeometric functions with semantic macros because they used the matrix and array environments in their arguments, while the DLMF only uses \atop for the same visualization. Consequently, none of our replacement patterns matched even though we correctly identified the expressions as hypergeometric functions. Entries 3 (from above) and 54, illustrate how minor errors already cause a failure in the semantic enhancement process. In the DLMF, the elliptic integral only uses a comma to separate the arguments. Hence, the appropriated semantic macro did not match . Similarly, the hypergeometric function in entry 54
inappropriately uses commas to split the arguments. Hence, again, none of the replacement patterns matched the expression. For an appropriate translation, one must derive the 1 and 2 from in order to extract the correct arguments.
One idea for solving these issues is to add more replacement rules to a macro. Greiner-Petter et al.[9] presented a search engine for MOI that allows searching for common notations for a given textual query. Searching for Jacobi polynomials in arXiv.org shows that different variants of are highly related or even equivalently used for Jacobi polynomials, such as p, H, or R rather than P. However, widening the replacement patterns further may harm performance, as seen in Table 2 (in the paper) for higher numbers of retrieved noun phrases and macros.
Derivatives and Prime Notations
Related problems that we encountered with our implementation of replacement patterns are primes and derivative notations. Primes for differentiation are generally put in between the function identifier and its argument, e.g., . Unfortunately, this causes the replacement patterns to fail because Ai(var1) did not allow tokens in between. We can avoid this by adding support for optional tokens to our pattern matching implementation. Hence, we would rather generate the pattern Ai opToken (var1).
The DLMF adds primes between the semantic macro and its arguments as well, e.g., \AiryAi'@{z}. Hence, we can also simply put this optional token into the semantic LaTeX expression.
Synonyms
One minor issue we faced were synonyms. For example, entry 51 discusses Kravchuk polynomials while the DLMF using the different transliteration Krawtchouk polynomials. Hence, our pipeline was unable to find the correct semantic macro for the polynomials. Since we already use Elasticsearch (ES) to search for semantic macros, and ES is capable of handling synonyms, we only need to feed the database with common synonyms. In this case, the Wikipedia article itself mentions the alternative transliteration at the beginning of the article. We could extract these synonyms while analyzing the Wikitext and adding them to the semantic macro database.
References
- ↑ 1.0 1.1 Moritz Schubotz and Alexey Grigorev and Marcus Leich and Howard S. Cohl and Norman Meuschke and Bela Gipp and Abdou S. Youssef and Volker Markl, "Semantification of Identifiers in Mathematics for Better Math Information Retrieval", In: Proceedings of the 39th International ACM SIGIR conference on Research and Development in Information Retrieval (SIGIR), 2016, Pisa, Italy, July 17-21, 2016
- ↑ 2.0 2.1 2.2 M. Schubotz, L. Krämer, N. Meuschke, F. Hamborg, and B. Gipp, "Evaluating and Improving the extraction of mathematical identifier definitions", In: CLEF. Volume 10456. Springer, 82-94. DOI: 10.1007/978-3-65813-1_7.
- ↑ 3.0 3.1 H. Cohl, A. Greiner-Petter, and M. Schubotz, "Automated symbolic and numeric testing of DLMF formulae using computer algebra systems." In: CICM. Volume 11006. Springer, 39-52. DOI: 10.1007/978-3-319-96812-4_4
- ↑ Giovanni Yoko Kristianto and Goran Topic and Akiko Aizawa, "Utilizing dependency relationships between math expressions in math IR", In: Information Retrieval Journal, 20.2 (2017).
- ↑ 5.0 5.1 Luis Espinosa Anke and Steven Schockaert, "Syntactically Aware Neural Architectures for Definition Extraction", In: Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT, New Orleans, Louisiana, USA, June 1-6, 2018, Volume 2 (Short Papers)
- ↑ 6.0 6.1 Deyan Ginev and Bruce R. Miller, "Scientific Statement Classification over arXiv.org", In: Proceedings of The 12th Language Resources and Evaluation Conference (LREC), 2020, Marseille, France, May 11-16, 2020
- ↑ Natalia Vanetik and Marina Litvak and Sergey Shevchuk and Lior Reznik, "Automated Discovery of Mathematical Definitions in Text", In: Proceedings of The 12th Language Resources and Evaluation Conference (LREC), 2020, Marseille, France, May 11-16, 2020
- ↑ Dongyeop Kang and Andrew Head and Risham Sidhu and Kyle Lo and Daniel S. Weld and Marti A. Hearst, "Document-Level Definition Detection in Scholarly Documents: Existing Models, Error Analyses, and Future Directions", In: Proceedings of the First Workshop on Scholarly Document Processing, SDP@EMNLP 2020, Online, November 19, 2020
- ↑ André Greiner-Petter and Moritz Schubotz and Fabian Müller and Corinna Breitinger and Howard S. Cohl and Akiko Aizawa and Bela Gipp, "Discovering Mathematical Objects of Interest - A Study of Mathematical Notations", In: WWW'20: The Web Conference, Taipei, Taiwan, April 20-24, 2020